CS275

HW 03

Structured Lists

Due: Monday, February 25

The goals for this assignment are increasing your skills with

For this assignment you will again work together in groups of 2 or 3. You must work in a group, even if you don't like it; single submissions will be docked a signficant number of points. Each group will produce one solution file. Put the following comment at the top of the file:

; Homework 3 
; names of the members of your group 
Save the file as "hw3.ss".

Your group should solve each of the exercises in the following way. One person will act as "scribe" for the problem. The scribe's job is to enter the code into the computer, along with several test examples. The scribe role should rotate around the group so that everyone has a chance to do it an equal number of times. All members of the group should participate in writing each solution, and deciding on test cases. Try to ensure that your test cases are comprehensive; don't use only the test cases provided to check your code.

You can use the solution to any exercise as a helper function in subsequent exercises.

Assume the following data types for input to the functions:

a, b, c ... atoms (numbers or symbols)
n, m, ... numbers
lat A list of atoms
lyst A list of any kind
llyst A list of lists
vec A list of numbers (a vector)
mat A matrix -- a list of lists, all of the same length, which make up the rows of the matrix. In this lab the matrix entries will be numbers; in other labs they may be other objects.
exp Any expression (atom or list)

Exercises

  1. Write (firsts llyst) and (rests llyst). For both of these llyst is a list of lists. (firsts llyst) returns a new list with the cars of each element of llyst; (rests llyst) returns a new list with the cdrs of each element of llyst.
    • (firsts '( (a b c) (d e f) (g h i) ) ) returns (a d g)
    • (rests '( (a b c) (d e f) (g h i) ) ) returns ( (b c) (e f) (h i) )

  2. Write three functions that break off parts of a list: (firstN n L) returns the first n entries of L; (middle m n L) returns the m entires of L starting after the nth. (tail n L) returns the portion of L that comes after the nth entry
    • (firstN 3 '(1 2 3 4 5 6 7 )) returns (1 2 3)
    • (middle 2 3 '(1 2 3 4 5 6 7)) returns (4 5)
    • (tail 3 '(1 2 3 4 5 6 7)) returns (4 5 6 7)

  3. Write (addvec vec1 vec2), where vec1 and vec2 are vectors (lists of numbers) with the same length. This returns a vector containing the sums of the corresponding elements of vec1 and vec2.
    • (addvec '(1 2 3) '(4 5 6) ) returns (5 7 9)
    • (addvec '( ) '( ) ) returrns ( )

  4. Write (dot-product vec1 vec2), where again vec1 and vec2 are vectors with the same length. This returns the sum of the products of the corresponding elements of vec1 and vec2.
    • (dot-product '(1 2 3) '(4 5 6) ) returns 32 (= 1*4 + 2*5 + 3*6)
    • (dot-product '( ) '( )) returns 0

  5. Write (dot-row vec mat), where the length of vec is the same as the length of each row of mat. This returns a vector containing the dot-product of vec with each row of mat.
    • (dot-row '(1 2 3) '((1 4 7) (2 5 8) (3 6 9)) ) returns (30 36 42)

  6. Write (transpose mat), which returns the transpose of mat. This interchanges the rows and the columns of mat, i.e., the first row of mat is the first column of the transpose, the second row of mat becomes the second column of the transpose, and so forth. Hint: use firsts and rests.
    • (transpose '((1 2 3) (4 5 6)) ) returns ((1 4) (2 5) (3 6) )

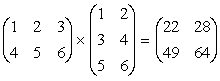
  7. Write (matmult mat1, mat2), which returns the matrix product of mat1 and mat2. The entry of the ith row and jth column of the product is the dot-product of row i of mat1 and column j of mat2. For this to make sense the lengths of the rows of mat1 must be the same as the lengths of the columns of mat2. For example, matrix product
    • (matmult '((1 2 3) (4 5 6)) '((1 2) (3 4) (5 6)) ) returns ((22 28) (49 64))

      Hint: use a helper function that works with mat1 and the transpose of mat2. This helper function makes a lot of use of dot-row.

  1. Write (occur a L), which returns the number of times atom a occurs in the general list L.
    • (occur  'y  '(x y z z y) ) returns 2
    • (occur  'y '(a (x (y)) (((y)) y z)) returns 3
    • (occur 'y  '( ) ) returns 0


  2. Write (flatten L) that takes a list L and creates a flat list wth the same elements.
    • (flatten   '(x y z z y) ) returns(x y z z y)
    • (flatten   '(a (x (y)) (((y)) y z)) returns (a x y y y z)

  3. Write (insertion-sort vec), which returns a vector with the elements of vec in sorted order.
    • (insertion-sort  '(5 8 9 1 3) ) returns (1 3 5 8 9)

    Note that there is a built-in sort function; The Scheme Programming Language discusses it in section 12.2. Don't use it. I want you to do insertion-sort just using basic Scheme functions.