CS275

HW 05

Fun with Trees

Due Wednesday, March 19

For this assignment you will write a number of programs that involve trees. Recall that a tree is a data structure that is either empty, or contains some data and has 0 or more children, each of which is a tree.

Scheme s-expressions can be used to construct the tree datatype. For now we will use a fairly informal approach; soon you will learn about a Scheme mechanism that can be used to define precise abstract datatypes.

At the beginning of the following section the tree datatype will be defined. The exercises in the section will all make use of that datatype in their solutions.

This may be done as a collaborative assignment with up to 3 students per group, as in HW 3, or as an individual assignment.

The goals for this assignment are to

Download this file Put the following comment at the top of your Dr. Racket file:

; Homework 5 
; the name or names of people who worked on this assignment 
Here is a starter file for this lab. It contains all of the tree code that is listed below. Save this file as "Lab5.ss".

Introduction -- the tree structure

A tree is either

  1. an empty tree, which has no fields
  2. a non-empty tree, which has a value field containing a number and a list-of-children field containing a list of children of the node, which are themselves trees.

With this in mind we use define-datatype to create the tree datatype, and include some additional functions to manage the tree type. This code also includes a sample tree.


(require (lib "eopl.ss" "eopl"))

; definition of tree datatype
(define-datatype tree tree?
        (empty-tree)
        (non-empty-tree (value number?) (list-of-children (list-of tree?))))

; recognizer provided by define-datatype
; (tree? x)

; recognizers for empty-tree and non-empty-tree
(define empty-tree?
       (lambda (tr)
              (cases tree tr (empty-tree () #t)
              (else #f))))

(define non-empty-tree?
        (lambda (tr)
               (cases tree tr
                       (non-empty-tree (value list-of-children) #t)
                       (else #f))))

; constructors provided by define-datatype
; (empty-tree)
; (non-empty-tree v list-of-children)

; Convenience constructor

(define makeTree
        (lambda l
               (non-empty-tree (car l) (cdr l))))

; destructors (accessors)

(define value
        (lambda (tr)
               (cases tree tr
                       (empty-tree () (eopl:error 'value "empty trees have no value"))
                       (non-empty-tree (value list-of-children) value))))

(define children
        (lambda (tr)
               (cases tree tr
                      (empty-tree () (eopl:error 'value "empty trees have no children"))
                      (non-empty-tree (value list-of-children) list-of-children))))

; other useful functions

(define number-of-children
        (lambda (tr)
        (length (children tr))))

(define leaf?
        (lambda (tr) (zero? (number-of-children tr))))

; example trees

(define Empty (empty-tree))
(define T1 (makeTree 50))
(define T2 (makeTree 22))
(define T3 (makeTree 10))
(define T4 (makeTree 5))
(define T5 (makeTree 17))
(define T6 (makeTree 73 T1 T2 T3))
(define T7 (makeTree 100 T4 T5))
(define T8 (makeTree 16 T6 T7))

For example, here is a picture of T8 showing the others as subtrees:

 

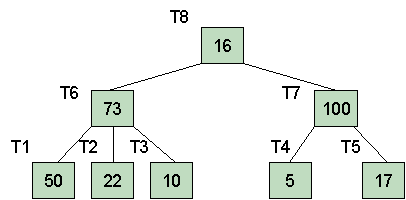
We can view T8 as a list: (16 (73 (50) (22) (10)) (100 (5) (17))). Be sure that you can see how the tree structure is preserved in this list.

Click here to download this file. You should rename is Lab5.ss and use it to start your solutions file.


In the exercises that follow, you should use the mapping functions map and fold (and, if necessary, apply) with higher-order functions to make your solution as concise as possible. You should also use letrecto define any recursive help functions.

All programs should be written using the tree operators defined above. You should rarely need to use car, cdr, cons or null

As usual, if the solution to an earlier problem is useful in a later one, go ahead and use it.

Exercises:

In all of these tr is a value of the tree datatype

Exercise 1: (childSum tr)

This returns the sum of the values in hte children of the given node.. The tree is assumed to be non-empty.

(childSum T8) returns 173
(childSum T6) returns 82

Exercise 2: (allSum tr)

This sums the entire set of values found in the tree. If tree is empty it returns 0.

(allSum T8) returns 293
(allSum T6) returns 155

Exercise 3: (tree->list tr )

This converts a tree into a list format

(tree->list T8) returns (16 (73 (50) (22) (10)) (100 (5) (17)))

Exercise 4: (list->tree l)

This is the inverse of tree->list.

(tree->list (list-> tree '(16 (73 (50) (22) (10)) (100 (5) (17))))) returns (16 (73 (50) (22) (10)) (100 (5) (17)))

Exercise 5: (visitTree f tr)

Here f is a function of 1 numerical variable. This returns a new tree with the same structure only every value v in tree has been transformed to (f v).

(tree->list (visitTree (lambda (x) (* x 3)) T1)) returns (150)
(tree->list (visitTree (lambda (x) (* x 3)) T8)) returns (48 (219 (150) (66) (30)) (300 (15) (51)))

Exercise 6: (sizeof tr)

This returns the number of elements in the subtree rooted at the given node.

(sizeof T6)) returns 4
(sizeof T8) returns 8


Exercise 7: (height tr)

Returns the height of the tree. Assume that the empty tree has height 0, a single-node tree has height 1, etc.

(height T1) returns 1
(height T8) returns 3

Exercise 8: (count n tr)

Returns the number of times value n appears in the tree.

(count 22 T8) returns 1
(count 7 T8) returns 0

 

Exercise 9: (preorder tr) and Exercise 10: (postorder tr)

Each of these produces a flat list of the values in the tree. They differ only in the order in which the values are listed:

  • (preorder tr) lists the value at the root ahead of the values of the children. 
             (preorder T8) returns (16 73 50 22 10 100 5 17)
  • (postorder tr) lists the value at the root after the values of the children. 
             (postorder T8) returns (50 22 10 73 5 17 100 16)