Tries
A trie is a multiway search tree based on the idea that a key
value can often be written as a string of digits or characters.
It's also known as a radix tree
or a digital search tree.
A trie can be used to implement a set. Set is a
java
interface with the following fundamental operations (among
others):
- boolean add(Object object); // add the object to the set,
if it is not already in the set. Return value is true if and
only
if
the set is modified as a result of this operation.
- boolean contains(Object object); // returns true if and
only if the set contains the given object.
The trie is structured as follows: Suppose we have a set of
numbers expressed with a given radix (base) r. Each node has r
children, one for each possible value of the radix. A number is
stored in a node based
on its radix r representation. For example, in a base 10 tree,
the
number 274 would be stored in a node which is the 4th child of its
parent, which is the 7th child of its parent, which is the second
child
of its parent, which is the root. Each node also has a boolean
flag to indicate whether or not a value is stored at this node.
A trie can be used to hold a set of character strings, by considering
the characters to be the digits of a number whose radix is the number
of characters in the alphabet. For example, we can consider
strings of the letters "a" through "z" to be numbers written with
radix
26.
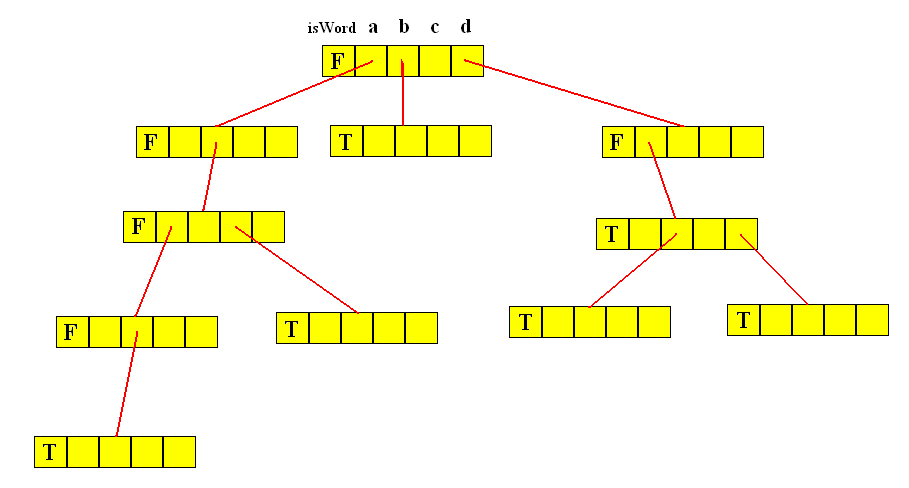
Consider the following Trie. It assumes an alphabet of the
letters { a, b, c, d } and holds the strings "b", "abc" "abab", dad",
"da", and dab. All slots which do not contain a red link contain
the value "null".
Searching the Trie
To search for a given string with characters c0,
c1,
..., cn-1:
- Start at the root (level 0)
- At level i, follow the link to the (ci)-th child of
the node.
- If you find a null pointer before arriving at level n, then the
string is not found in the trie.
- If you arrive at a node at level n, then the isWord flag in that
node indicates whether or not the word is in the set..
Inserting a word in a Trie
To insert a word in a trie:
- Follow the same path (starting at the root) that you would follow
in searching for the word.
- If you hit a null pointer along the way, replace the null
pointer
with a pointer to a new node, set the new node's isWord flag to
"false",
and continue.
- When you reach level n, set the "isWord" flag to true.
Analysis:
What does an empty Trie look like? Can the null string ("") be
inserted in a Trie?
What is the order of the running time of the search and insert
operations? How does this compare with a binary search
tree?
Are there any disadvantages to the use of a trie as a Set?
How much space is used by a trie? How does this compare with a
binary search tree?
Could a trie be used to implement the Map interface?
How would you write a program to traverse a trie; that is, visit each
word stored in the trie, in lexicographic order?
Lecture notes courtesy of John Donaldson
