CS 150 - PreLab 08

This week you'll be making sounds and music with Python. In this prelab, you will think about some of the underlying details of the lab itself. There are 3 numbered questions here.

Part 0 - Headphones

This lab is going to involve music; while some of the lab computers do have speakers, not all do, and regardless, it'll get a little crazy if everyone is trying to play sound files at the same time. So please bring a pair of headphones to lab. You won't be constantly listening through them, so any kind of earphones or earbuds will be fine.

Part 1 - Music Basics

keyboard Notes are musical sounds called "pitches", that is, how high or low the note is. For example, do, re, mi are all pitches (also known as C, D, and E). Notes can be defined relative to each other; you can raise or lower the pitch by whole steps by going from one note to the next, or the pitch can be raised and lowered in half steps using sharps (#) and flats (b), respectively. These half-steps are called semitones, and there are 12 semitones in an octave (for example, the half step from C to C# is a semitone; from C# to D is as well). Each note also has a duration (how long it sounds) and a volume (how loud it sounds), so technically, a "note" is defined not only by its pitch, but also by its duration and volume.

Part 2 - Some Physics of Music

A music note is just a sound wave. More specifically, any one note can be thought of as a sine wave, and is characterized by its [regular] frequency of oscillation (pitch), its amplitude (volume), and its length (duration). Each of these is explained below.

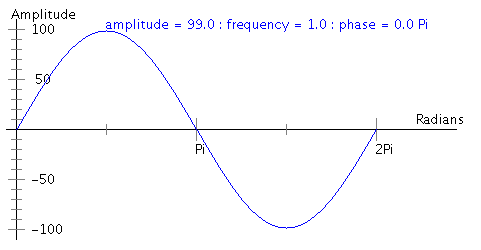	y(t) = 99 * sin(t) for 0<=t<=2Pi
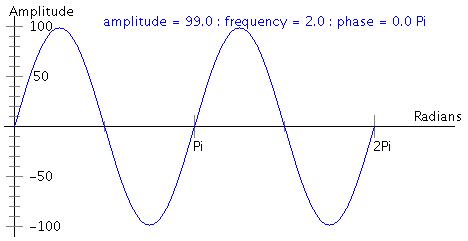	y(t) = 99 * sin(2t) for 0<=t<=2Pi
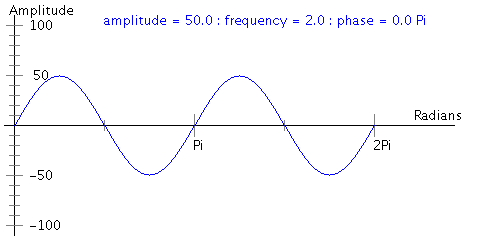	y(t) = 50 * sin(2t) for 0<=t<=2Pi

Frequency (Pitch)

The frequency of a sine wave is the number of peaks per 2Pi radians. The first wave above has frequency 1, and the following two waves have frequency 2.
The way that humans perceive pitch is associated with the frequency of the sound wave which impinges upon the ear. A high pitch sound corresponds to a high frequency sound wave (many peaks in a small span), and a low pitch corresponds to a low frequency sound wave (few peaks in a small span).
More specifically, frequency is vibrations per second. The unit used to measure frequency is the Hertz (abbreviated Hz), where 1 Hertz = 1 vibration / second. The human ear can detect sound waves with frequencies ranging from 20Hz to 20000 Hz.
Doubling a pitch's frequency increases the pitch by an octave, and halving it decreases it by an octave. There are 12 semitones in an octave, therefore, the ratio between the frequency of successive semitones is the 12th root of two (1.05946) (NOTE: this is not the same as 1 + 1/12). That is, to increase a pitch by a semitone, you only need to multiply its frequency by the 12th root of 2.

1) Use the above information to fill in the frequencies of the pitches below. There is a single semitone step from each note to the next.

A	A#	B	C	C#	D	D#	E	F	F#	G	G#	A
440.00	466.16											880.00

Amplitude (Volume)

The amplitude of a sine wave is the maximum height (above 0) of any peak. The first two waves above have amplitude 99, the last wave has amplitude 50.
The greater the amplitude, the LOUDER the sound.

Length (Duration)

The length of a sine wave is, well, the length along the x-axis of the wave. The waves above have length 2Pi.
The longer the length, the longer the duration of the sound. One second of sound corresponds to length 2Pi.

Multiple notes

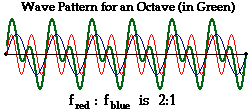
Each wave corresponds to a note. To play mutliple notes, you just superimpose (that is, add) the waves of each individual note. In the example below, the blue wave represents the low note, the red wave represents the note one octave higher (its frequency is double that of the blue wave), and the green wave represents both notes playing at the same time (the sum of their waves).

Constructing Sound Waves

To construct a sound wave, you first need to know the frequency (H), the amplitude (A), and the length (T) of your wave. Once you have this information, you just need to calculate y(t) = A * sin( 2 Pi H t ) for all 0 <= t <= T. Note that t is the timestep of the note you are calculating.

Notice that y(t) is a continuous function (you can draw it without lifting your pen), and computers work naturally with discrete rather than continuous data. To reprsent a sound wave we sample the wave many times per second.. Each sample represents the amplitude (y-value) of the sound wave at a particular instant in time (t). The sampling rate is the number of samples taken per second. Audio from CDs typically uses a sampling rate of 44100. So, instead of drawing the sound wave without lifting your pen, the computer is drawing a whole lot of dots along the same wave, with the idea that if you draw enough dots, it still looks (and sounds) like a continuous wave even though it isn't. The same idea is used in animation and those little flip books; a sequence of still frames when played at a high enough speed give the impression of smooth/continuous movement. So now if you are calculating 2 seconds of audio with a sampling rate of 44100, the values for t will be 0,1,2,3,...,88198,88199,88200.

2) Suppose we have variables amp representing the amplitude of a sound, samplerate representing the rate at which we sample the soundwave, duration representing the length of this sound in seconds, and halftone indicating the note (0 for middle C, -3 for A, +3 for D, and so forth). The equation of our soundwave is

f(t) = amp*sin(2*pi*freq*t/samplerate)

where freq is 440*2**((halftones+3)/12)

Use this to write a Python loop that computes valuse for f(t) as t vareis from 0 to samplerate*duration and stores them in a list L.

In the lab, you will be writing your own Soundwave class that will represent the discretization of a snippet of sound. This loop will provie the bulk of your Soundwave constructor.

Part 3 - Making Beautiful Music

Once you've gotten a basic Soundwave class defined, much of the remainder of the lab revolves around producing music. In particular, we're going to use .wav files (a type of sound file type, much like an .mp3) to produce a variety of scales and even generate a Minuet and Trio.

A scale is a sequence of notes, defined by the intervals between them. For example, the major scale is defined by the 7 intervals (and hence 8 notes) (2,2,1,2,2,2,1), that is, there are 2 semitones between the first and second notes, between the second and third notes, but a single semitone between the third and fourth notes, and so on. The C major scale is the major scale starting at C and is thus the sequence of notes of values starting at around 523 and ending around 1046, that is, the notes (C, D, E, F, G, A, B, C). The D major scale is the major scale starting at D: the sequence of notes (D, E, F#, G, A, B, C#, D).

There are many other interesting scales, such as the minor scale, defined by the intervals (2,1,2,2,1,2,2), and the blues scale, defined by the intervals (3,2,1,1,3,2) (the scale only contains 7 notes).

3) Suppose you are given a scale, defined by its tonic (starting) note, which has offset T from middle C, and intervals (I1, I2, I3,..., In) (that is, the second note of the scale is I1 semitones from the tonic note, the third note of the scale is I1+I2 semitones from the tonic, etc.). List the offsets for the n+1 notes of the scale. [ Don't overthink this. The first note has offset T, the second T+I1, etc,] Our Soundwave class will have a constructor that takes as an argument a note's offset from middle C, so to play a scale we just need to make a Soundwave object for each of the offsets of the scale.

Finally, let's talk about this Minuet and Trio business. What is a Minuet and Trio? It is musical piece that is often the third movement of a sonata in the Classical (Mozart and Haydn) style.. Both the Minuet and Trio follow a specific rhythm and form, and they are usually combined by first playing the Minuet, then playing the Trio, then the Minuet once more. You can listen to a very nice Minuet and Trio here.

You'll be generating a Minuet and Trio based on a random algorithm developed by Mr. Mozart himself. Your Minuet will contain 16 measures (musical snippets), as will your Trio. For each of the 16 measures in the Minuet, you will randomly generate a number between 0 and 10 (inclusive); you will use this number to pick a specific music snippet from the following table (there are 176 total snippets). That is, for each column in the table below, you will randomly pick a row, and use whichever measure is that (column, row) entry. For example, if I generate the 16 random numbers (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4, 5) for the Minuet, then I will select the snippets (32, 95, 113, 45, 154, 133, 169, 123, 102, 20, 26, 56, 73, 160, 1, 151) from the Minuet table. Here is such a randomly generated Minuet and Trio. For the Trio, you do the same thing except your random number is between 0 and 5, inclusive.

	Minuet Measures
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	96	22	141	41	105	122	11	30	70	121	26	9	112	49	109	14
1	32	6	128	63	146	46	134	81	117	39	126	56	174	18	116	83
2	69	95	158	13	153	55	110	24	66	139	15	132	73	58	145	79
3	40	17	113	85	161	2	159	100	90	176	7	34	67	160	52	170
4	148	74	163	45	80	97	36	107	25	143	64	125	76	136	1	93
5	104	157	27	167	154	68	118	91	138	71	150	29	101	162	23	151
6	152	60	171	53	99	133	21	127	16	155	57	175	43	168	89	172
7	119	84	114	50	140	86	169	94	120	88	48	166	51	115	72	111
8	98	142	42	156	75	129	62	123	65	77	19	82	137	38	149	8
9	3	87	165	61	135	47	147	33	102	4	31	164	144	59	173	78
10	54	130	10	103	28	37	106	5	35	20	108	92	12	124	44	131

	Trio Measures
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
0	72	6	59	25	81	41	89	13	36	5	46	79	30	95	19	66
1	56	82	42	74	14	7	26	71	76	20	64	84	8	35	47	88
2	75	39	54	1	65	43	15	80	9	34	93	48	69	58	90	21
3	40	73	16	68	29	55	2	61	22	67	49	77	57	87	33	10
4	83	3	28	53	37	17	44	70	63	85	32	96	12	23	50	91
5	18	45	62	38	4	27	52	94	11	92	24	86	51	60	78	31

Honor Code

If you followed the Honor Code in this assignment, write the following sentence attesting to the fact at the top of your homework.

I affirm that I have adhered to the Honor Code in this assignment.

	Minuet Measures
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	96	22	141	41	105	122	11	30	70	121	26	9	112	49	109	14
1	32	6	128	63	146	46	134	81	117	39	126	56	174	18	116	83
2	69	95	158	13	153	55	110	24	66	139	15	132	73	58	145	79
3	40	17	113	85	161	2	159	100	90	176	7	34	67	160	52	170
4	148	74	163	45	80	97	36	107	25	143	64	125	76	136	1	93
5	104	157	27	167	154	68	118	91	138	71	150	29	101	162	23	151
6	152	60	171	53	99	133	21	127	16	155	57	175	43	168	89	172
7	119	84	114	50	140	86	169	94	120	88	48	166	51	115	72	111
8	98	142	42	156	75	129	62	123	65	77	19	82	137	38	149	8
9	3	87	165	61	135	47	147	33	102	4	31	164	144	59	173	78
10	54	130	10	103	28	37	106	5	35	20	108	92	12	124	44	131

	Trio Measures
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
0	72	6	59	25	81	41	89	13	36	5	46	79	30	95	19	66
1	56	82	42	74	14	7	26	71	76	20	64	84	8	35	47	88
2	75	39	54	1	65	43	15	80	9	34	93	48	69	58	90	21
3	40	73	16	68	29	55	2	61	22	67	49	77	57	87	33	10
4	83	3	28	53	37	17	44	70	63	85	32	96	12	23	50	91
5	18	45	62	38	4	27	52	94	11	92	24	86	51	60	78	31

	Minuet Measures
	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	96	22	141	41	105	122	11	30	70	121	26	9	112	49	109	14
1	32	6	128	63	146	46	134	81	117	39	126	56	174	18	116	83
2	69	95	158	13	153	55	110	24	66	139	15	132	73	58	145	79
3	40	17	113	85	161	2	159	100	90	176	7	34	67	160	52	170
4	148	74	163	45	80	97	36	107	25	143	64	125	76	136	1	93
5	104	157	27	167	154	68	118	91	138	71	150	29	101	162	23	151
6	152	60	171	53	99	133	21	127	16	155	57	175	43	168	89	172
7	119	84	114	50	140	86	169	94	120	88	48	166	51	115	72	111
8	98	142	42	156	75	129	62	123	65	77	19	82	137	38	149	8
9	3	87	165	61	135	47	147	33	102	4	31	164	144	59	173	78
10	54	130	10	103	28	37	106	5	35	20	108	92	12	124	44	131

	Trio Measures
	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
0	72	6	59	25	81	41	89	13	36	5	46	79	30	95	19	66
1	56	82	42	74	14	7	26	71	76	20	64	84	8	35	47	88
2	75	39	54	1	65	43	15	80	9	34	93	48	69	58	90	21
3	40	73	16	68	29	55	2	61	22	67	49	77	57	87	33	10
4	83	3	28	53	37	17	44	70	63	85	32	96	12	23	50	91
5	18	45	62	38	4	27	52	94	11	92	24	86	51	60	78	31

PreLab 09