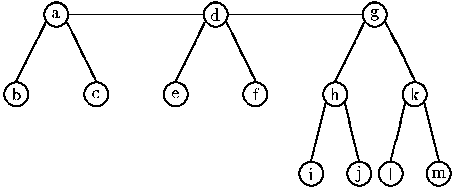
Figure 3 from page 2 of Okasaki's paper (Null children of leaves not shown)
Traditional lists are the bread and butter of functional programmers, however for a few important operations they are not very efficient. Namely to access the ith element requires O( i ) time. For this reason Chris Okasaki developed the random-access list which he describes in his paper Purely Functional Random-Access Lists
. Here is an order comparison between various structures, operations and the random-access list.
| List | Array | Random-Access List | |
|---|---|---|---|
| cons | O( 1 ) | O( n ) | O( 1 ) |
| head | O( 1 ) | O( 1 ) | O( 1 ) |
| tail | O( 1 ) | O( n ) | O( 1 ) |
| look up | O( i ) | O( 1 ) | O( log n ) |
| update | O( i ) | O( 1 ) | O( log n ) |
In fact the bounds for the random-access list can be shown to be better than this (see Okasaki's paper).
The random-access list is traditionally implemented as a forest (a list of trees). Where each tree is complete and in preorder. The trees are held in increasing order in the main list. This allows the representation of any size array and the appropriate operations in the necessary order times(see Okasaki's paper for details).
The structure of the random-access list proposed by Okasaki can be visualized like so:

Note that this requires at least three types of node. The root node
of the trees which has two children and a sibling (also a tree size). The second, the branch node
, forms the main structure of the trees and has only two children. The third is the null node
which is necessary to represent the empty list and terminate the branches of the trees (some programmers may even go so far as to add a leaf node
which has no children only data).
This many node types makes the code to implement the random-access list more complex and longer. Before reading Okasaki's paper I developed and implemented another form of the tree. His paper mentions this form in passing, when considering Myers' random-access stacks without redundant pointers, and that it is isomorphic to his. This structure can be visualized as:
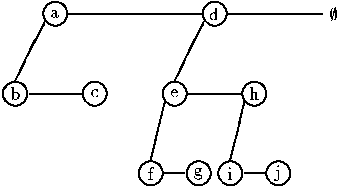
Notice that this requires only the main node type and a null node. All order times are preserved and the code is simplified. The one draw back is that the tree size must be stored in each node, taking more space. However, the space used is on the same order has the original structure.
I have implemented an immutable version of this structure in Scheme. All operations are supported except update which is left out for simplicity but could be added. This is not a necessary feature of this form of the structure. A single special instance of the node is designated as the null or empty node. This is similar to the Singleton Design Pattern found in object-oriented designs (see Design Patterns Gamma et. al.)
 |
jwalker@cs.oberlin.edu |