Self-Balancing Binary Search Tree

by, Jeff Walker

As a winter term project (Jan. 2000) I worked with professor Stephen Wong at Oberlin College on developing an object oriented implementation of a Self-Balancing Binary Search Tree. This was an extension of work done previously by him and other students to develop object oriented binary tree structures, thus I began from code provided by him. However, as we worked together many changes were made to this system to produce the resulting code. Although it was assumed the major challenge would be finding a measure of balance and representing that in the tree, it was in fact more difficult to develop a proper set of relations between types of trees and their methods.

Interfaces

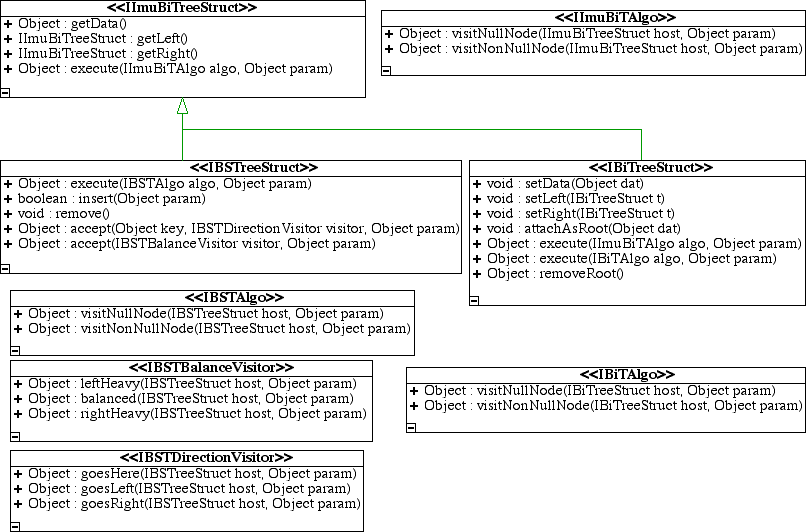
After working with the binary tree (BiT) and binary search tree (BST) for some time it was realized that a BST was not a BiT or vice versa. Initially the BST had been implemented in terms of the BiT, however it was necessary to hide the BiT because it had less restrictions on how one would modify the tree. After struggling with this it became apparent that they were not equivalent. Indeed that there was a missing parent. When all possible operations were listed for both the BiT and BST the parent was then a tree which had all their common properties. The methods of each are as follows:

*Table 1*
BiT	BST	Unknown Parent
`getData`	`getData`	`getData`
`getLeft`	`getLeft`	`getLeft`
`getRight`	`getRight`	`getRight`
`execute(Parent Algorithm)`	`execute(Parent Algorithm)`	`execute(Parent Algorithm)`
`setData`
`setLeft`
`setRight`
`attachAsRoot`
`execute(BiT Algorithm)`
	`remove`
	`insert`
	`execute(BST Algorithm)`
	`accept(Balance Visitor)`
	`accept(Direction Visitor)`

The parent which has only those methods which are common to both a BiT and BST is an immutable binary tree. This relationship was then implemented in the classes and allowed algorithms for the immutable parent to run on both BSTs and BiTs. The relationship is now more clearly expressed as the relationships between the interfaces to each type of tree. Thus separating the implementation and interface aspects (this is necessary do to things which will be discussed later).

Fig. 1

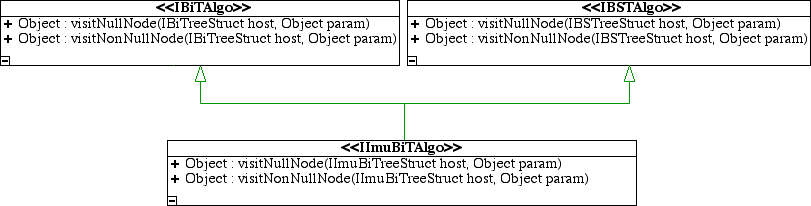
Note that the return types of both getLeft and getRight should be lower for the BiT and BST but Java does not yet have covariant return types and so explicit type casts are needed (Update: this will be added to java when generics are). Another inexpressible but more unusual relationship is found between the executes of each tree and the algorithms they run. Each algorithm has essentially the same methods but takes different parameter types. This causes duplicate executes in the child trees. It seems there is some relationship between these interfaces and methods which is not expressible in Java. It has been proposed that a subclass could have parameters which were a super class of the parameters of the method it overloaded (so called contravariant parameter types). This would not break the type system in any way. This is often rejected as not being useful. However, imagine for a second that Java allowed this (though it would cause ambiguity when mixed with method overloading that would have to be resolved). If this were possible then the immutable binary tree algorithm would implement both the BST Algorithm and BiT Algorithm (see Fig. 2). This would work since in both cases it's methods take a super class of those it would now be implementing. Now BST and BiT would have one execute (the ones they currently have) which would override the execute inherited from the immutable tree since immutable binary tree algorithms are now subclasses of BST Algorithm and BiT Algorithm and we are allowing parameters to be of a super class to the ones they are over riding. This scheme would seem to work and may point at something needed in object oriented languages. Yet, this relationship between the algorithm visitors seems awkward.

Fig. 2

Another relationship that is not clear from the interfaces is between the direction visitor and the balance visitor. Both have the same three methods only with different names. Some thought was given to combining them into one visitor because of this. However they do not have equivalent meaning. One, the direction visitor, is based off the data in the tree and it's relation to a key value. The other, the balance visitor, is based solely on the balance state of the tree. Because of the very different meaning of the two it was decided that they were two different things and this would prevent using the wrong algorithm in the wrong instance. One unanswered question is whether the direction visitor should be modified to have only two methods. One method for the case when the key matches the object found at this node and one where the key goes to the left or right. In which case it would be called with the left or right sub-tree as its host, as appropriate.

The relationship between the immutable tree, BiT and BST was unexpected. It raises interesting questions about the relation between functional and object oriented approaches, their appropriate use, and ultimate oneness. The relation between visitors hints at currently inexpressible relationships and suggests an important area of research in object oriented language design. This is especially the case if visitors are indeed a central part of all object oriented programming. It would seem that issues like this would come up whenever there was a family of related visitors which visited a family of hosts.

Implementation

In order to reuse code the BiT and BST were implemented in terms of the immutable binary tree. This is not strictly necessary since the introduction of interfaces for all the trees involved. However, it demonstrates an interesting relationship between them. In order to allows this the immutable tree had to be constructed with all the trappings of being mutable. Namely it had a state pattern and methods for setting data, left, and right. All this was completely hidden from all but the child classes. The child classes then made use of this already existent architecture. This also leads to sub-classing on a much larger scale then is commonly done in OOP. Instead of a single class extending another, a system of classes was extending another. The tools necessary to easily do this are not yet available and it makes the implementation seem more complex then it probably really is. Also, since only the parent held the state of a node. It was necessary for the children to constantly get the state and down cast it. An action they could do safely since the super was set up to allow them to be the only class which could create the state. This concept is currently expressed through a number of seemingly unrelated methods. However, it seems important enough that some thought should be given to better express this. Namely that a subclass can safely restrict the type of a property of its parent when the parent behaves appropriately.

Global v.s. Local

Within the binary tree there are themes of both local and global action. Traditionally remove and insert are thought of as global. The ordering of the whole tree is also global. Getting information from the tree, such as the data at a node and the left and right is an entirely local action. These seem to comprise the fundamental actions that are appropriate for a BST. The global relationship within the tree were originally expressed as a wrapper over the whole tree which enforced these global constraints. It also prevented visitors from entering the tree because at that time the tree was still implemented in terms of a BiT which would have exposed methods that it is invalid to use on a BST. In these scheme extra data was held as a wrapper on the data (not a decorator because it could not be made invisible). As work continued, this was replaced by each node having a link to the root node of a tree. This change allowed visitors to come into the tree (since it was now not implemented in terms of BiT) and perform various actions some of which could have a global affect. It was at this time realized that remove was at least in part a local event and not global. Instead of providing a key for the item to be removed a node could have remove called on it directly. The sub-tree below it would then be reshaped accordingly and a message sent out toward the root to adjust the tree above that node. However, the adjusting only was required along the direct path from the removed node to the root. Also, this adjusting had to be done from the lower parts of the tree upward. At this time it was brought up that there may be more than one piece of data in the tree that matched a key. So this was an inappropriate method of finding the place of the removed node. This is when a bold step was made. The link to a root node was changed into a link to the parent. This allows remove to be a completely local event which simply sends messages up the tree as well. One problem with this is it is necessary for a node to know or deduce which side of its parent it is attached to. Right now this is done through various logic. It would be advisable to rework the tree to allow symmetry to solve the problem. Also, it may be possible to make insert local. Currently a message is sent up the tree to the root from which an insert algorithm is run. The algorithm however simply puts the node in an appropriate place at the bottom of the tree and calls for the adjusting of the tree as does remove. Perhaps insert could be allowed at null nodes and that would cause the tree to re-balance itself. This does not answer how to insure that the trees global order is preserved.

Balancing

The BST is self balancing. That is to say that when an insert or remove happens, such that the tree's global order is maintained the tree automatically reacts to bring itself into balance. At this time the state of balance is defined to be when all nodes in the tree have no more than a difference of 1 between the number of nodes in their left and right sub trees. When a remove occurs, the value at the removed node is replaced either by the max of the left tree or the min of the right tree, the direction does not matter however the tree will not require as much balancing if it is taken from the heavier side. In the case that one side is the null node then the other side is what replaces this, in the case that both sub trees are null, the removed node is transition to the null state. The min or max is removed (note that this forms a recursive definition.) Then a message is sent up the tree toward the root, indicating at each level that a side has gotten lighter. If any node is shifted out of balance by this, it shifts to correct it (as discussed later) then passes the message up the tree. Note also that when a remove occurs in the middle of the tree it causes a remove lower in the tree. Only the second remove causes a message to be sent up the tree. Since only one node is really removed, the node in the middle simply has it's data replaced.

An insert is accomplished in similar fashion, an algorithm is triggered on the root which traverses the tree using the data to be inserted as a key. When it reaches a null node it inserts the data there and causes a message to pass up the tree informing all nodes in a direct line above that one that the side has become heaver. If a node is shifted out of balance by this action it shifts to regain balance then passes the message back up the tree.

When a node is thrown out of balance by an insert or remove it preforms a shift to regain balance. Namely, it inserts the data at that node to the lighter side, then pulls up the max or min (as appropriate to the side it is pulling from) to the current node. Note that this may cause more nodes below it to require shifting. However, it will not require any node above it to shift since the total number of nodes in that sub tree have not changed.

These are the fundamental mechanisms by which the tree self balances. They seem to be exactly the right way to accomplish the self balancing. They reflect the recursive nature of the tree in there own recursive definition (i.e. an insert or remove could trigger both a insert or a special remove and so on). Some work needs to be done in order to make the system more symmetric. If this is done then the problem of self balancing is basically answered.

A notion of balancing strategies has been proposed. A balancing strategy would simply be a strategy used to decide when to preform a shift at a node and what direction to shift. It should be trivial to implement this system. For example a strategy could be written which defined balanced such that the total tree could not have a difference of more than one between its maximum and minimum depth. The one limitation to this is that all the node truly knows is the number of nodes in its left and right sub trees. The above example would be accomplished by assuming each tree below you was balanced in that manner and using node counts to determine whether a tree level should be full.

Conclusions

My work on self balancing binary trees has advanced many new questions. I believe these questions are pushing in a good direction. It is no longer simply a matter of how self balancing should be implemented, but what the proper actions are on a BST and how they behave. In essence, what a binary search tree really is. Also, what is the relationship of the BST to other data structures? These questions push toward a unification of all data structures in a Grand Theory of Data Spaces. This theory would bring to light the proper nature of each data structure now know and express their relationships. It may also bring new data structures into existence. These questions must be answered by computer scientists before they can begin to truly understand their field. In addition, the problems encountered with the BST implementation have also shed light on places of research as yet unexplored in the area of object oriented languages and design.

jwalker@cs.oberlin.edu