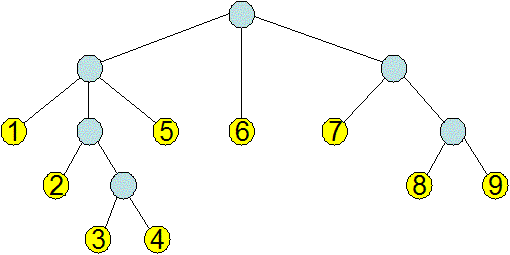
The file tree.ss is a module containing the definition of a simple n-ary tree. In this tree model only leaf nodes contain values, which will be numerical. Each interior node contains only one field, children, a list of nodes. This tree structure is in fact isomorphic to the ordinary Scheme list of numbers. The file includes the function build-tree, which converts a number list into a tree, and there is a sample tree called tree1 (depicted below). For the sake of simplicity, error checking and the "empty tree" are not included.

Take a moment to look at this definition.
We are interested in implementing the function (traverse tree leaf-visitor), where leaf-visitor is a function of 1 variable. This function runs through the entire tree, invoking leaf-visitor whenever it arrives at a leaf.
A typical leaf visiting activity might be to print the value.
(define leaf-visitor
(lambda (z)
(printf "~s~n" (leaf-node-value z))))
A simple algorithm (written in pidgen pseudocode) for tree traversal goes like this:
The last line of this description is kind of awkward. To simplify the code, let's write our recursive routine so that it assumes a list of trees (usually the children of some node), focusing on the car of that list as the current child of interest. We'll call the recursive function try for reasons that will be made clear later.traverse(tree, visit): if tree is a leaf, then visit(tree) else traverse(child, visitor) for each child in children(tree)
traverse(tree, visit) = try(list(tree))
where
try(trees):
if (null?(trees)) then do nothing
else begin
if car(trees) is a leaf then visit(car(trees))
else try(car(trees));
try(cdr(trees))
end
Convince yourself that the two versions really describe the same algorithm.
We would like to convert the help function try to CPS. First, notice that the body of try is a sequence of 2 steps:
Because step 1 can involve a recursive call (if the current node is an interior node) traverse is not tail-recursive. This means the CPS version will be non-trivial. Our job is to find the "on-the-way-out" part of the non tail-recursive call and make it into a continuation. But this is just step 2, which carries the computation on to the remaining children. Moreover, since there is no value passed from step 1 to step 2, our continuation can be a function of no arguments. Once again, for reasons to be made later, we'll call such a continuation a failure continuation and use letter q to represent it.
The CPS version of the program has the following form:
(define traverse-q
(lambda (tree leaf-visitor)
(let try ([tree-list (list tree)]
[q (lambda () 'done)])
(if (null? tree-list) ...
(let* ([current (car tree-list)]
[rest (cdr tree-list)]
[new-q ...]
(if (leaf-node? current)
(leaf-visitor current new-q)
(try (interior-node-children current) new-q))))))))
In addition to the nodelist, try now takes a failure
continuation which initially returns "done". Step 2 has been
eliminated (where did it go?). Note that leaf-visitor also
includes a failure continuation parameter. The "q-equivalent" to
our previous leaf-visitor example is
(define leaf-visitor-q
(lambda (z q)
(printf "~s~n" (leaf-node-value z))
(q)))
(define leaf-visitor-q1
(lambda (z q)
(printf "~s~n" (leaf-node-value z))
q))
What can you do with traverse-q that you couldn't do with traverse?
We aren't done with traverse yet. Notice the similarity between the 2 alternatives (leaf-visitor (leaf-node-value current) new-q) and (try (interior-node-children current) new-q) in the body of traverse-q. Each takes a value and failure continuation. Let's use the term success continuation for such a function. In fact, we can insist that the "value" part always be a node. Rewriting our program we get
(define traverse-kq
(lambda (tree leaf-visitor)
(let try ([tree-list (list tree)]
[k leaf-visitor]
[q (lambda () 'done)])
(if (null? tree-list) ...
(let* ([current (car tree-list)]
[rest (cdr tree-list)]
[new-k ...]
[new-q ...]
(if (leaf-node? current)
(k current new-q)
(new-k current new-q)))))))
We see that
((if (leaf-node? current) k new-k) current new-q)
Finally, we will convert the success and failure continuations in the program to true Scheme continuations. Here is the answer; you'll need it later.
(define traverse-cc
(lambda (tree leaf-visitor)
(let/cc
exit
(let ([topq (let/cc return (let/cc q (return q)) (exit 'done))])
(call-with-values
(lambda ()
(let/cc
topk
(let try ([tree-list (list tree)]
[k topk]
[q topq])
(if (null? tree-list) (q)
(let* ([current (car tree-list)]
[rest (cdr tree-list)]
[new-k (let/cc
return
(call-with-values
(lambda () (let/cc k1 (return k1)))
(lambda (node new-q)
(try (interior-node-children node) k new-q))))]
[new-q (let/cc
return
(let/cc q1 (return q1))
(try rest k q))])
((if (leaf-node? current) k new-k) current new-q))))))
leaf-visitor)))))
This one is very tricky. We are using something new here, call-with-values, which allows us to return 0 or more values and pass
them on as arguments to a waiting function. Continuations
automatically work with call-with-values. See chapter 2.2 in
the mzscheme manual on the help desk.Test this one out with leaf-visitor-q1.