Each of the exercises in this section work with a tree structure, which we define below. You may solve these exercises in collaborative groups of up to 3 members and submit one solution for the group, or as an individual effort and submit your own solution. Please be sure to indicate the names of all participants as a comment.
We will consider trees that store a numerical value at each node, and have an arbitrary number of children. This tree type is defined as a variant record:
Tree definition
With this in mind we use define-datatype to create the tree datatype, and include some additional functions to manage the tree type. This code also includes a sample tree.
empty tree no fields non-empty tree has a value field, containing a number, and a list-of-children field, containing a list of the children of the node
; treestruct.scm -- defines tree datatype for Lab 6
(require (lib "eopl.ss" "eopl"))
; definition of tree datatype
(define-datatype tree tree?
(empty-tree)
(non-empty-tree (value number?) (list-of-children (list-of tree?))))
; recognizer provided by define-datatype
; (tree? x)
; recognizers for empty-tree and non-empty-tree
(define empty-tree?
(lambda (tr)
(cases tree tr
(empty-tree () #t)
(else #f))))
(define non-empty-tree?
(lambda (tr)
(cases tree tr
(non-empty-tree (value list-of-children) #t)
(else #f))))
; constructors provided by define-datatype
; (empty-tree)
; (non-empty-tree v list-of-children)
; Convenience constructor
(define makeTree
(lambda l
(non-empty-tree (car l) (cdr l))))
; destructors (accessors)
(define value
(lambda (tr)
(cases tree tr
(empty-tree () (eopl:error 'value "empty trees have no value"))
(non-empty-tree (value list-of-children) value))))
(define children
(lambda (tr)
(cases tree tr
(empty-tree () (eopl:error 'value "empty trees have no children"))
(non-empty-tree (value list-of-children) list-of-children))))
; other useful functions
(define number-of-children
(lambda (tr)
(length (children tr))))
(define leaf?
(lambda (tr) (zero? (number-of-children tr))))
(define tree->list
(lambda (tr)
(cases tree tr
(empty-tree () '())
(non-empty-tree (value list-of-children) (cons value (map tree->list list-of-children))))))
; example tree
(define Empty (empty-tree))
(define T1 (makeTree 50))
(define T2 (makeTree 22))
(define T3 (makeTree 10))
(define T4 (makeTree 5))
(define T5 (makeTree 17))
(define T6 (makeTree 73 T1 T2 T3))
(define T7 (makeTree 100 T4 T5))
(define T8 (makeTree 16 T6 T7))
Click here to download this file.
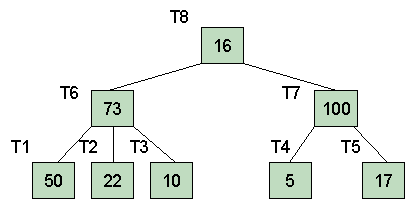
Here is a picture of T8, showing the others as subtrees

Using tree->list, we can view T8 as a list: (16 (73 (50) (22) (10)) (100 (5) (17))). Be sure that you can see how the tree structure is preserved in this list.
Solution Technique
In the exercises that follow, you should use the mapping functions map and fold (and, if necessary, apply) with higher-order functions to make your solution as concise as possible. You should also use letrec to define any recursive help functions. Recursion on globally defined functions is permitted if help functions are not required.
All programs should be written using the tree operators defined above. You should rarely need to use null?, car, cdr or cons. Try to avoid using them when you can.
If you are not sure whether map, fold, etc. are appropriate, first solve the problem in "Little Schemer" style, then see if your solution fits the design pattern of one or more mapping functions.
Similarly, you may first want to define your help functions globally; then once you have everything working redefine them using letrec.
As usual, if the solution to an earlier problem is useful in a later one, go ahead and use it.
Here again are the definitions of map (a letrec version) and fold. map already exists in Scheme as a primitive, so you don't have to include it in your file (it's shown here to help you recognize its design pattern). Include the definition of fold at the top of your answer file.
(define map
(lambda (proc lyst)
(letrec ([help-map
(lambda (l)
(if (null? l)
'()
(cons (proc (car l)) (help-map (cdr l)))))])
(help-map lyst))))
(define fold
(lambda (recur-case base-case lyst)
(letrec ([help-fold
(lambda (l)
(if (null? l)
base-case
(recur-case (car l) (help-fold (cdr l)))))])
(help-fold lyst))))
You can download treestruct.scm and use it to start your solution file
General Hints
If l is the list () and f is a function of 1 argument, then (map f l) returns the list (). You will generally want to use map to apply the same function to all the children of a tree node.
Similarly, if l is the list () and f is a function of 2 arguments, then (fold f base l) produces . You will generally use fold to "collect" the values produced after using map.
Apply may be needed when you have a list of data that you want to use as the arguments to a function. One place this can arise is when calling makeTree. You can avoid the problem by using the non-empty-tree constructor instead.
Take care that your functions are of the right type (e.g. the functional argument to map must be a function of one argument).
Important Advice: Think Recursively!
Trees are highly recursive structures. When solving each problem:
Sample Exercise
(childValues tree)
returns the list of values at the of tree (tree is assumed to be nonempty). Note: does not include the value at the root.
(childValues T8) → (73 100) (childValues T6) → (50 22 10)
Solution
(define childValues
(lambda (tree)
(map value (children tree))))
Inverse of tree->list.
(tree->list (list-> tree '(16 (73 (50) (22) (10)) (100 (5) (17))))) → (16 (73 (50) (22) (10)) (100 (5) (17)))
Returns the sum of the values at the children of tree. (tree is assumed to be non-empty).
(childSum T8) → 173 (childSum T6) → 82
Sums the entire set of values found in the tree. If tree is empty returns 0.
(allSum T8) → 293 (allSum T6) → 155
where f is a function of 1 numerical variable. Returns a new tree in which every value v in tree has been transformed to (f v).
(tree->list (visitTree (lambda (x) (* x 3)) T1)) → (150) (tree->list (visitTree (lambda (x) (* x 3)) T8)) → (48 (219 (150) (66) (30)) (300 (15) (51)))
Returns a new tree in which all values have been incremented by 1. The empty tree is returned unchanged.
(tree->list (upTree T8)) → (17 (74 (51) (23) (11)) (101 (6) (18))) (tree->list (upTree T1)) → (51)
where f is a function of 1 numerical variable. Returns a procedure, which when given a tree, returns a new tree in which every value v in tree has been transformed to (f v).
(define addOneToAll (visitTree-maker add1)) (tree->list (addOneToAll T8))→(17 (74 (51) (23) (11)) (101 (6) (18)))
Returns the height of the tree. Assume that the empty tree has height 0, a single-node tree has height 1, etc.
(height T1) → 1 (height T8) → 3
Each of these produces a flat list of the values in the tree. They differ only in the order in which the values are listed:
where visit-fn is a function of 1 numerical value and co-fn is a function of 2 arguments. Folds co-fn over base-value and the preordered list consisting of the results produced by invoking visit-fn on the values in tree. Returns base-value on the empty tree.
(visitAndCollect (lambda (x) (* x x)) + 1 T7) → 10315 (visitAndCollect (lambda (x) (> 0 x)) (lambda (x y) (or x y)) #f T8) → #f (visitAndCollect (lambda (x) (> 0 x)) (lambda (x y) (or x y)) #f (visitTree (lambda (z) (if (> z 50) (- z) z)) T8)) →#t
(allSum-vac tree)
Identical to allSum.
(preorder-vac tree)
Identical to preorder.
(someValueIs pred tree)
where pred is a predicate. Returns #t if some value of tree satisfies pred; #f otherwise
(someValueIs (lambda (x) (< x 100)) T6) → #t (someValueIs (lambda (x) (< x 0)) T8) → #f
(allValuesAre pred tree)
where pred is a predicate. Returns #t if all values of tree satisfies pred; #f otherwise
(allValuesAre (lambda (x) (< x 100)) T8) → #f (allValuesAre (lambda (x) (> x 0)) T6) → #t