Chinese Ring Puzzle Applet

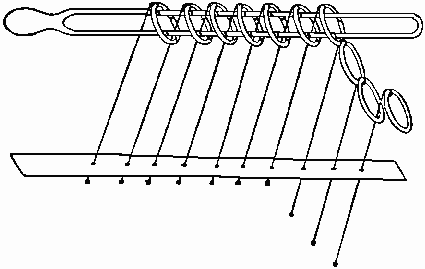
Chinese ring Puzzle

The above picture is of a famous puzzle known as the Chinese Ring Puzzle (aka. The Devils Needle Puzzle aka. Cardan's rings). As practise with recursion I decided to implement a java program which would recursively solve the puzzle.

Explanation of the Applet

Each ring may be considered to be in one of two states up or down, other states are possible but not productive.

Up:

A ring is up if the top segment of the ring comes up over the long piece, this can also be thought of as an interlocked state. (On)
Down:

A ring is down if the whole ring is below the long piece or the piece is free to move so that it is not over the ring, this can be thought of as the free state. (Released)

In order to remove the center long piece all the rings must be put into the down state. To put the piece all the way back on all the rings must be put into the up state. To make a state transition it is necessary to move the middle piece near to that ring which can be done only if the rings "after" it are in a particular state.

To put a ring up: The ring after it must be Up
and any ring after that must be Down
To put a ring down: The ring after it must be Up
and any ring after that must be Down
The last ring: The last ring may be put Up
or Down at any time

This problem is very easy when expressed as a recursive problem. To put a ring into a state which it is not in is simply to put the rest into the ready state (first ring up, rest down) the base case is the last ring which may be put up or down any time.
How the Puzzle is Modeled Through Objects

To a computer scientist the structure used to model the puzzle will most closely resemble a linked list. For this reason a puzzle is represented by a RingList object. The RingList class uses a modified composite pattern so that it represents the first ring in the list and then holds when appropriate a rest which is itself a RingList. If it were a normal composite pattern then one would expect to see an abstract ring list with concrete ring and final (or null) ring subclasses. The problem this has which is the same problem that most list implementations have is that then a list node can't change from null to non-null. Most of the time this doesn't seem important, however consider the case in which one has a null list and wants to insert an element into it. A Lisp style cons (append a new head) won't work because then others who share the list with you won't have access to the inserted element. Thus the null node must become a non-null node in order to contain the inserted data. This frequently known as dynamic reclassification and when called for the best solution is usually the state design pattern. Thus each RingList has a ARingState (here the convention is that an abstract classes' name is prefixed by an 'A'). The two concrete states are NonNullRingState and NullRingState which are subclasses of ARingState. This structure and its implementation were discussed by Nguyen and Wong in their paper Patterns for Decoupling Data Structures and Algorithms. When first attempting to model the problem one is tempted not to have a null ring but instead a final ring. I attempted this first but found the code to be far more complicated than seemed proper. Once reimplemented using a null ring the design was simpler and easier to understand. This shows that though not included in the Design Patterns book by Gamma et. al. the null pattern is an important one.

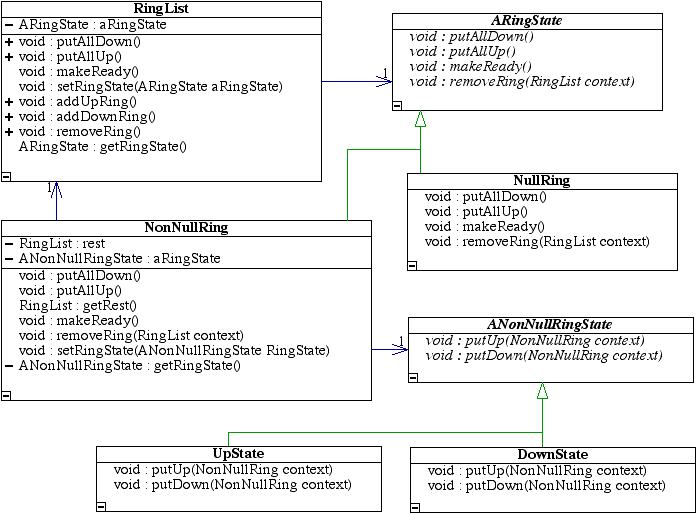
This doesn't completely model the problem since any ring in a NonNullRingState must also be in either the up or down states. For this reason each NonNullRingState has a ANonNullRingState object which is in fact either a UpState or DownState. This is the second use of the state pattern.

That explains the object structure necessary to model the problem, but what behaviors do these objects have. Clearly a RingList must be able to add and remove rings, and put all rings in it up or down (solve the puzzle). The other less obvious necessary behavior is to be able to put a RingList into the ready state (first ring up rest down) so that a ring before it can change state. Other possible behaviors include allowing the traversal of the RingList, but those are not necessary for this simple example. Each of these behaviors becomes methods of the RingList class. They all delegate to the state has one would expect in a state pattern. Adding and removal of rings is handled directly in the null and non-null ring states (see Patterns for Decoupling Data Structures and Algorithms). Putting rings up or down is handled at both null vs. non-null and up vs. down state levels since for example some behavior is invariant to a non-null ring whether it is in the up or down state so that behavior is in the non-null state class. The null state simply ignores all request relating to moving rings up or down. Below is listed code snippets from all relevant methods.

In NonNullRing:
void putAllDown()
{ getRingState().putDown(this);
getRest().putAllDown();
}

void putAllUp()
{ getRingState().putUp(this);
getRest().putAllUp();
}

void makeReady()
{ getRingState().putUp(this);
getRest().putAllDown();
} 		In NullRing:
void putAllDown()
{
}

void putAllUp()
{
}

void makeReady()
{
}
In UpState:
void putUp(NonNullRingState context)
{ //Do nothing, we are already up
}

void putDown(NonNullRingState context)
{ context.getRest().makeReady();
context.setRingState(new DownState());
} 		In DownState:
void putUp(NonNullRingState context)
{ context.getRest().makeReady();
context.setRingState(new UpState());
}

void putDown(NonNullRingState context)
{ //Do nothing, we are already down
}

jwalker@cs.oberlin.edu